
Sum and Product of Roots of Quadratic Equation Now, check out the formulas to find the sum and the product of the roots of the equation. D Based on the discriminant value the nature of the roots of the quadratic equation can be predicted. The value b 2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'.

This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation.
QUADRATIC FORMULA SOLVER HOW TO
Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation. The roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation. This is good for us, because now we can take square roots to obtain: The left-hand side is now a perfect square: Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a) 2 on both sides: To determine the roots of this equation, we proceed as follows: Proof of Quadratic FormulaĬonsider an arbitrary quadratic equation: ax 2 + bx + c = 0, a ≠ 0 This formula is also known as the Sridharacharya formula.Įxample: Let us find the roots of the same equation that was mentioned in the earlier section x 2 - 3x - 4 = 0 using the quadratic formula. Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = /2a. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation. The two roots in the quadratic formula are presented as a single expression. There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. Quadratic formula is the simplest way to find the roots of a quadratic equation. Maximum and Minimum Value of Quadratic Expression Solving Quadratic Equations by Factorization
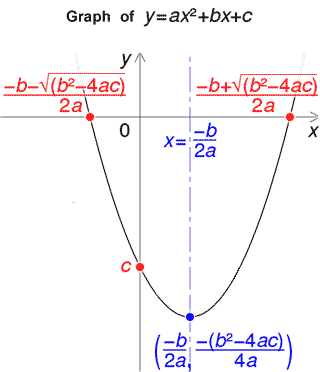
Nature of Roots of the Quadratic Equation We shall learn more about the roots of a quadratic equation in the below content. These two solutions (values of x) are also called the roots of the quadratic equations and are designated as (α, β). Quadratic equations have maximum of two solutions, which can be real or complex numbers. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy, etc. In other words, a quadratic equation is an “equation of degree 2.” There are many scenarios where a quadratic equation is used. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. Quadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0.


 0 kommentar(er)
0 kommentar(er)
